![]()
Elektronische Datenverarbeitung (EDV) beruht im wesentlichen auf der Verarbeitung von Zahlen. Daher werden Zahlensysteme benötigt, die sich für diese Art der Datenverarbeitung eignen. Im folgenden soll zunächst der Aufbau von Zahlensystemen anhand des Dezimalsystems dargestellt werden.
 Dezimalsystem
Dezimalsystem
Das Dezimalsystem kennt entsprechend seiner
Zahlenbasis zur Zahlendarstellung 10 Zahlzeichen (0...9).
Als Beispiel schauen wir uns die (besondere) Zahl 365 an. Sie
ist zusammengesetzt aus den drei Zahlzeichen 3, 6 und 5. Die "Grösse"
der Zahl ergibt sich nicht aus der Addition der einzelnen Stellen,
sondern aus der Addition der mit ihrer Wertigkeit multiplizierten
Stellenl. Man spricht auch von der Einer-, der Zehner-
und der Hunderterstelle. Entsprechend können diese Wertigkeiten
auch in Exponentialschreibweise mit der Basis 10 dargestellt
werden: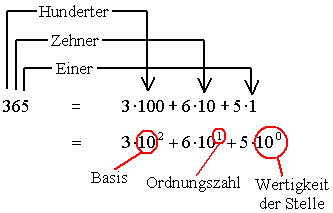
Bei der dezimalen Zählweise wird bei Erhöhung des Zählwertes zunächst die Einerstelle erhöht. Wird das größte Zahlzeichen 9 erreicht, wird die Einerstelle auf 0 gesetzt und die Zehnerstelle um eins erhöht. Dieser Vorgang setzt sich mit der Zehner-, Hunderter-, Tausenderstelle usw. fort.
Diese Beschreibung erscheint zunächst trivial, da jeder Mensch mit dieser Zählweise groß geworden ist. Sie ist jedem so verinnerlicht, dass er im täglichen Gebrauch von Zahlen nicht mehr darüber nachdenken muss, wann eine Stelle auf 0 gesetzt und die nächst Höhere erhöht werden muss. Würden EDV-Systeme im Dezimalsystem rechnen, wäre dies sicherlich von großem Vorteil.Vielleicht wäre selbst der größte Computerhasser nicht mehr ganz so negativ eingestellt. Der größte Vorteil wäre aber sicherlich, dass Daten im gleichen Zahlensystem eingegeben, ausgegeben und verarbeitet werden könnten.
Warum arbeiten EDV-Systeme nicht mit Dezimalzahlen?
Zahlen werden in der elektronischen DV durch
Spannungswerte dargestellt. Stellen wir uns ein einfaches System
zur Datenübertragung vor, wie es in jedem Computer vorhanden
sein muss. Um unsere Zahl 365 zeitgleich vom Empfänger
zum Sender zu übertragen wird für jede Stelle (Einer,
Zehner, Hunderter) eine elektrische Leitung benötigt. Im Sender
wird der dezimale Zahlenwert zunächst in einen äquivalenten
Spannungswert gewandelt. 0 = 0V, 1 = 1V, 2 = 2V ... 9 = 9V. Dieser
Spannungswert muss im Empfänger wieder als entsprechender Zahlenwert
interpretiert werden. Es ist leicht einsehbar, dass die Unterscheidung
von 10 unterschiedlichen Spannungswerten nur mit relativ hohem technischen
Aufwand zu meistern ist.
Um unsere Zahl 365 zeitgleich vom Empfänger
zum Sender zu übertragen wird für jede Stelle (Einer,
Zehner, Hunderter) eine elektrische Leitung benötigt. Im Sender
wird der dezimale Zahlenwert zunächst in einen äquivalenten
Spannungswert gewandelt. 0 = 0V, 1 = 1V, 2 = 2V ... 9 = 9V. Dieser
Spannungswert muss im Empfänger wieder als entsprechender Zahlenwert
interpretiert werden. Es ist leicht einsehbar, dass die Unterscheidung
von 10 unterschiedlichen Spannungswerten nur mit relativ hohem technischen
Aufwand zu meistern ist.
Gesucht ist also ein computergerechtes Zahlensystem wo die Unterscheidung der Zahlenwerte (bzw. Spannungen) technisch problemlos zu realisieren ist. Das einfachste Zahlensystem ist das Dualsystem.

 Dualsystem
Dualsystem
Beim dualen Zahlensystem existieren nur die zwei Zahlzeichen 0 und 1. Entsprechend muss ein Computersystem auch nur zwei Spannungszustände unterscheiden können. Dies ist im einfachsten Fall Spannung nicht vorhanden (0V) und Spannung vorhanden (5V).
Der Aufbau des Dualsystems entspricht dem Aufbau des Dezimalsystems. Die Basis ist allerdings 2. Damit ergeben sich natürlich Unterschiede in der Wertigkeit der Stellen. So gibt es hier keine Einer-, Zehner- oder Hunderterstelle, sondern - wie das Beispiel unten zeigt - eine Einer-, Zweier-, Vierer-, Achterstelle usw.:
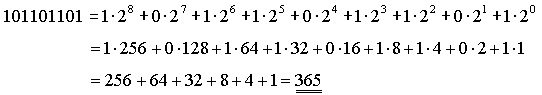
Hätten Sie sofort erkannt, dass die Dualzahl die Zahl der Tage pro Jahr darstellt? Keine Angst, dass ist reine Gewohnheit. Der Computer hat damit keine Probleme, er macht das seit seiner "Geburt"! Zur Übertragung der Zahl 365 im Dualcode benötigt das EDV-System einen "Datenbus" mit 9 elektrischen Leitungen. (Wie viele waren es noch mal im Dezimalsystem?..)
Die Umwandlung von Dualzahlen in Dezimalzahlen ist eigentlich ganz einfach, wenn man nur die Stellen mit ihrer Wertigeit addiert, die 1 sind. So ist 1100111001 = 29+28+25+24+23+20 = 512 + 256 + 32 + 16 + 8 + 1 = 825. Mit ein wenig Übung geht das wirklich leicht von der Hand!
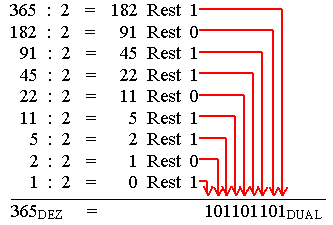 Umgekehrt verwendet
man für die Umwandlung von Dezimalzahlen in Dualzahlen häufig
das Resteverfahren. Die Dezimalzahl wird durch 2 geteilt und es
verbleibt als Rest 0 oder 1. Das Divisionsergebnis wird wieder durch
2 geteilt und auch hier wird der Rest notiert. Dies setzt sich solange
fort, bis das Divisionsergebnis 0 ist. Die "Reste" bilden
dann von unten nach oben gelesen die Dualzahl.
Umgekehrt verwendet
man für die Umwandlung von Dezimalzahlen in Dualzahlen häufig
das Resteverfahren. Die Dezimalzahl wird durch 2 geteilt und es
verbleibt als Rest 0 oder 1. Das Divisionsergebnis wird wieder durch
2 geteilt und auch hier wird der Rest notiert. Dies setzt sich solange
fort, bis das Divisionsergebnis 0 ist. Die "Reste" bilden
dann von unten nach oben gelesen die Dualzahl.
Ist man es gewohnt, kann man mit Dualzahlen die gleichen mathematischen Operationen durchführen wie im Dezimalsystem.
Addition von Dualzahlen
 Beim Addieren von
Dualzahlen wird analog zum Rechnen mit Dezimalzahlen vorgegangen.
Die Zahl wird Stellenweise von Rechts nach Links addiert. Ist die
Summe der Zahlen zu groß für eine Stelle, erfolgt ein
Übertrag in die nächste Stelle. Werden mehrere Zahlen
addiert, kann es auch Überträge in noch höhere Stellen
geben.
Beim Addieren von
Dualzahlen wird analog zum Rechnen mit Dezimalzahlen vorgegangen.
Die Zahl wird Stellenweise von Rechts nach Links addiert. Ist die
Summe der Zahlen zu groß für eine Stelle, erfolgt ein
Übertrag in die nächste Stelle. Werden mehrere Zahlen
addiert, kann es auch Überträge in noch höhere Stellen
geben.
Bei der Addition zweier dualer Ziffern ist der größte Wert 1 + 1 = 10 . Es erfolgt hier also ein Übertrag in die nächste Stelle. Werden drei Ziffern addiert, so kann 1 + 1 + 1 = 11 herauskommen. Die aktuelle Stelle ist 1 und es erfolgt ein Übertrag. Entsprechend gilt für 1 + 1 + 1 + 1 = 100. D. h. es erfolgt ein Übertrag in die übernächste Stelle.
Subtraktion von Dualzahlen 

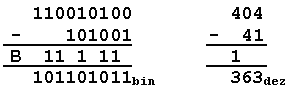 Beim Subtrahieren
wird ebenfalls bei der niederwertigsten Stelle (LSB=least significant
bit) begonnen. Ist die entsprechende Stelle des Minuenden kleiner
als die des Subtrahend, (also bei 0 - 1 ) muss von der nächst
höheren Stelle eine 1 "geborgt" werden. Der
Borger wird bei der nächsten Stelle dann zum Subtrahenden addiert.
Beim Subtrahieren
wird ebenfalls bei der niederwertigsten Stelle (LSB=least significant
bit) begonnen. Ist die entsprechende Stelle des Minuenden kleiner
als die des Subtrahend, (also bei 0 - 1 ) muss von der nächst
höheren Stelle eine 1 "geborgt" werden. Der
Borger wird bei der nächsten Stelle dann zum Subtrahenden addiert.
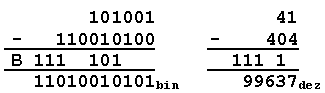 Ist der Subtrahend
insgesamt größer als der Minuend, gelangt man zur Zweierkomplement-
darstellung. Dies bedeutet, dass die Subtraktion unendlich
fortgesetzt werden kann, da am Ende jede neue Stelle wieder mit
einem Borger subtrahiert werden muss. Im Beispiel sind ab der 10.ten
Stelle (dual) alle Bits auf 1 zu setzen. Im Dezimalsystem
bedeutet dies, dass ab der 4.ten Stelle nur noch 9en stehen.
Ist der Subtrahend
insgesamt größer als der Minuend, gelangt man zur Zweierkomplement-
darstellung. Dies bedeutet, dass die Subtraktion unendlich
fortgesetzt werden kann, da am Ende jede neue Stelle wieder mit
einem Borger subtrahiert werden muss. Im Beispiel sind ab der 10.ten
Stelle (dual) alle Bits auf 1 zu setzen. Im Dezimalsystem
bedeutet dies, dass ab der 4.ten Stelle nur noch 9en stehen.
 Um die Zahl wie
gewohnt lesen zu können, gibt es zwei Möglichkeiten
zur Rückgewinnung des Zahlenwertes aus dem Zweierkomplement.
Um die Zahl wie
gewohnt lesen zu können, gibt es zwei Möglichkeiten
zur Rückgewinnung des Zahlenwertes aus dem Zweierkomplement.
1. Bei 2n-1 Stellen wird das Zweierkomplement
vom Wert 2n abgezogen.
Diese Lösung ist meist
jedoch unpraktikabel, da etwa in einem 8 Bit-System kein 9-Bit Zahlenwert
dargestellt werden kann.
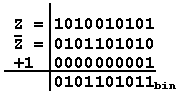 2. Die negative
Dualzahlen im Zweierkomplement wird stellenweise invertiert
und anschließend um 1 erhöht.
2. Die negative
Dualzahlen im Zweierkomplement wird stellenweise invertiert
und anschließend um 1 erhöht.
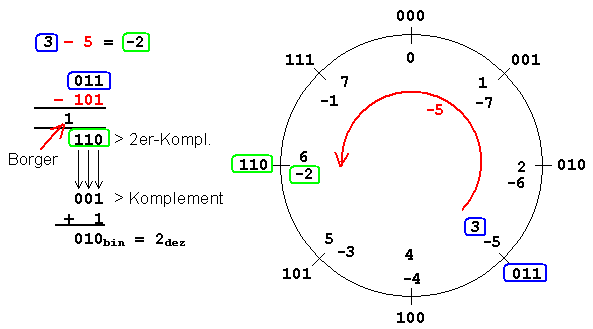
Dieser Vorgang wird besonders in der Darstellung der Dualzahlen in einem Zahlenkreis deutlich. Eine 3 stellige Dualzahl kann die Werte 000 - 111 annehmen. Die Addition 111 + 1 ergbäbe 1000. Diese Zahl ist aber mit 3 Bit nicht mehr darstellbar und wir erhalten daher als Ergebnis von 000. Man spricht hier von einem Überlauf. Dies ist der größte Albtraum eines jeden Programmierers und sollte dringlichst vermieden werden (die Assemblerprogrammierung kennt allerdings auch sinnvolle Anwendungen für den Überlauf!!). Die Subtraktion mit Zweierkomplementen kann am Zahlenkreis jetzt sehr anschaulich gezeigt werden.
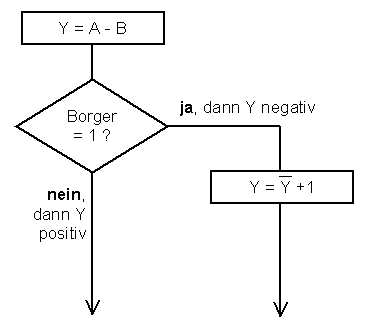
Am Borger (=1) lässt sich nach der
Subtraktion erkennen ob eine Zahl negativ ist. Die unten
abgebildete Rechenvorschrift (PAP) läßt sich in einem
Mikrocomputersystem sehr einfach realisieren, wie das abgebildete
Assemblerlisting zeigt. 
![]()
 Hexadezimalsystem
Hexadezimalsystem
Der Nachteil des Dualsystems ist, dass wir uns solche Zahlen sehr schlecht merken können. Sie sind nicht nur ungewohnt, sondern auch unübersichtlich. Wer kann schon etwas mit einer so langen Zahl 11111010100 anfangen. Zwar lässt sich die Gewohnheit nur sehr schwer ändern. Aber gegen die Unübersichtlichkeit von Dualzahlen gibt es ein Mittel. Hexadezimalzahlen (kurz: Hexzahlen) sind Zahlen mit der Basis 16. Es müssen daher auch 16 Zahlzeichen existieren. Dies sind die Ziffern 0 bis 9 und A bis F. Das ist natürlich mindestens so exotisch wie Dualzahlen. Hexzahlen haben aber einen entscheidenden Vorteil. Sie sind meist sehr kurz. So entspricht die Dualzahl 11111010100 der Hexzahl 7D4. Das ist natürlich viel einfacher zu merken, auch wenn wir die Bedeutung der Zahl erst nach der Umwandlung ins Dezimalsystem erkennen:
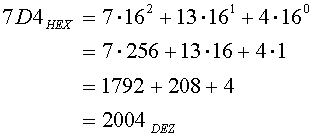
Der aufmerksame Beobachter erkennt, dass die Wertigkeiten der ersten, zweiten und dritten Stelle des Hexadezimalsystems mit der Wertigkeit der ersten, fünften und neunten Stelle des Dualsystems übereinstimmt (also 1, 16 und 256). Dies hat folgende praktische Konsequenz. Wenn bei einer Dualzahl der Übertrag auf die 5., 9., 13., 17. usw. Stelle erfolgt, dann erfolgt bei der Hexzahl entsprechend der Übertrag auf die 2., 3., 4., 5. usw. Stelle. Es lassen sich also immer 4 Bit einer Dualzahl zu einer Hexzahl zusammenfassen.
Dez |
Hex |
Dual |
|---|---|---|
0 |
0 |
0000 |
1 |
1 |
0001 |
2 |
2 |
0010 |
3 |
3 |
0011 |
4 |
4 |
0100 |
5 |
5 |
0101 |
6 |
6 |
0110 |
7 |
7 |
0111 |
8 |
8 |
1000 |
9 |
9 |
1001 |
10 |
A |
1010 |
11 |
B |
1011 |
12 |
C |
1100 |
13 |
D |
1101 |
14 |
E |
1110 |
15 |
F |
1111 |
16 |
10 |
10000 |
In der Tabelle kann man den Übertrag in die zweite Hexstelle von 15 nach 16 erkennen. Die Einer-Stelle wird 0 gesetzt und die 16er-Stelle um eins erhöht (also 1). Dort ist auch der Übertrag der Dualzahl in die fünfte Stelle. Die Umwandlung von Dualzahlen in Hexzahlen gestaltet sich mit Hilfe der obigen Tabelle (oder etwas Übung) sehr einfach.
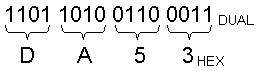
14.02.2005 |